Using an E6B Mechanical Flight Computer

Literally something you only need to do during primary training, to prove you CAN use an e6b. Sigh.

Density Altitude

For engine performance!

As you know, density altitude is pressure altitude adjusted for non-standard temperature. Standard temperature is 59° F, or 15° C at sea level.

Pressure altitude is true altitude adjusted for non-standard pressure. Standard pressure is 29.92 in. hg.

Pressure altitude is a really simple formula: pressure_altitude = (standard_pressure - pressure_setting) * 1000 + true_altitude

And while we can easily correct for non-standard temperature (the formula is: density_altitude = pressure_altitude + (120 * (outside_air_temperature - isa_standard_temperature))), it’s not as simple to do it manually, and an e6b is easy enough to use here.

Estimating isa standard temperature is ((true_altitude / 500) - 15) * -1

In the image below, the pressure altitude is 4500 feet, the true altitude is 4500 feet, and the outside air temperature is estimated to be 28° C. For the sake of the calculation, we bump that to 30° C. As you can see, the e6b then tells us that the density altitude is just over 7000 feet. Which we can double-check after a bit enough:

pressure_altitude = 4500 + (120 * (28 - (((4500 / 1000) - 15) * -1)))
 = 4500 + (120 * (28 - ((9 - 15) * -1)))
 = 4500 + (120 * (28 - (-6 * -1)))
 = 4500 + (120 * (28 - 6))
 = 4500 + (120 * 22)
 = 4500 + 2640
 = 7140

Which is about what the e6b tells us it us.

True Airspeed

True airspeed is effectively calibrated airspeed corrected for the density altitude.

So, in this case let’s re-use the earlier density altitude of ~7100 feet.

Calibrated airspeed then corresponds to the inner ring, and true airspeed the outer ring. That is, if your calibrated airspeed is 150 kts, then the true airspeed is ~167 kts.

Remember to correct for decimal placement.

Ground Speed

For a given true airspeed and heading, you can easily calculate your ground speed.

For this example, let’s say you are heading 270 at 125 knots, with the wind at 300 at 15 knots.

Set the center “dot” on the rear of the circle to some value - I pick 100 because it’s a nice round number. Set the circle (true index) to the wind direction (so… 300). Now, mark (IN PENCIL) the wind speed relative to the value you chose (place a mark where it says 115). Like so:

Now rotate so that the corrected heading is under the true index, and slide up so that the true airspeed is under the center dot. Like so:

Now we can read the ground speed (in this case, ~139 knots), and wind correction angle (~3 degrees, to the right - or fly heading 273).

When done, wipe the pencil lead off.

Time to travel distance

Now that we have a ground speed for this leg, we can calculate the time it takes to travel a given distance.

For this example, let’s say we have a ground speed of 100 kts, and the leg is going to be 13 nm.

Before we use the e6b, let’s do some quick mental math to estimate an acceptable range: 13 nm / 100 kts is just over 1/10 hour. Converting to minutes, it’s just over 6 minutes, but only just - this leg should take between 7 and 9 minutes.

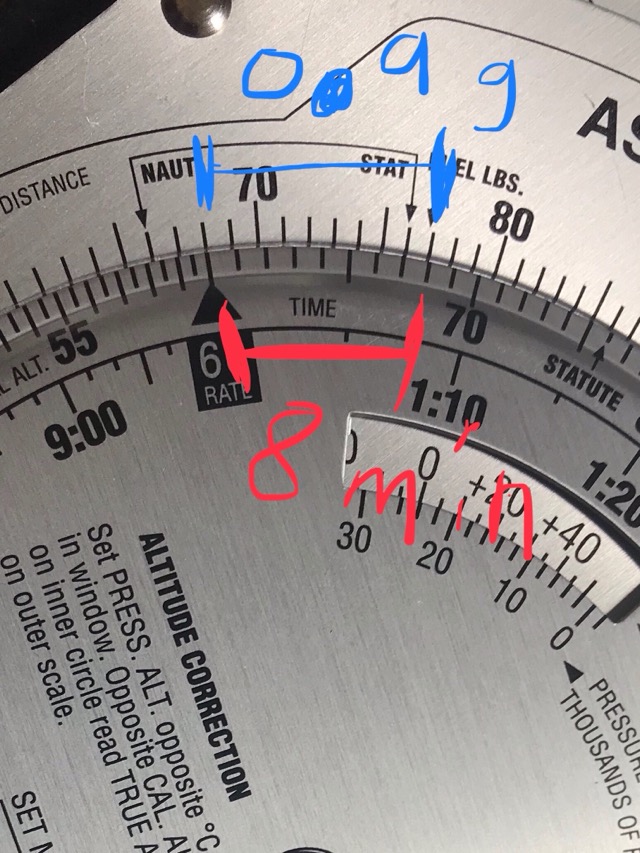
First thing we do to calculate this on an e6b is to align the “60 RATE” box on the inner circle with the approximate speed you’re going. In this case, it should be aligned with the “10” at the top.

Next, we count the distance from the “10” marker - 13 ticks from the marker, and compare that with the corresponding value on the “time” scale. This gives us our estimated time. In this case, it’s just under 8 minutes. As expected.

Of course, since we have the time (and a calculator handy) to do this, the actual estimated time is:

distance = speed * time
time = distance / speed
time = 13 nm / 100 kts
time = 0.13 hrs
time = 7.8 minutes

As expected.

Fuel usage

Now that we have time to travel a given distance, we can use the known rate of fuel consumption to calculate fuel usage.

For this, let’s assume fuel usage rate of 6.8 gph at cruise - a somewhat efficient Cessna. I’ll also use a time from the previous calculation.

We’ll mentally move the decimal point to the right one, to place the “rate” indicator at 68 on the calculator.

Now, on that same minutes time scale we used earlier, we count 8 minutes - or the amount of time we plan to travel that leg.

The gph usage then corresponds to the other side of that 8 minute marker - in this case, 9 ticks above the 68 tick. Keep in mind to move the decimal point back to the left, so that we use 0.9 gallons as our expect fuel usage.

Note that we could go the other way - if we had 10 gallons available, then we could move 100 ticks clockwise to get the number of minutes we can travel at that rate. (In this case, just under 2.5 hours). You can also compare to the inner “time scale” to get the value in hours instead of minutes.

Last updated: 2019-07-29 22:19:01 -0700